虚数の話(3)

極座標表示への動機

これまで$2+4i$とか表していた実軸と虚軸の平面（ガウス平面）のことを直交座標（ちょっこうざひょう）と呼ぶことがある。これのメリットは何と言っても足し算がしやすいというところにあった。何しろ各要素をそれぞれ足し算すればいい。

\begin{align}
(2+4i)+(-1+3i)&=(2-1)+(4+3)i\\
&=1+7i
\end{align}

視覚的にもこれらは矢印を足し合わせたものであって、イメージしやすいと思う。

しかし、これが掛け算になるとどうだろう？

\begin{align}
(2+4i)(-1+3i)&=2×(-1)+2×3i+4i×(-1)+4i×3i\\
&=-2+6i-4i-12\\
&=-14+2i
\end{align}

計算はできるが、これが何を表しているのかはさっぱりわからない。それは、直交座標と複素数の掛け算の相性が悪いからであって、別の表し方をすれば掛け算の意味ももっと明瞭になる。今から導入したいのは極座標（きょくざひょう）と呼ばれる座標の表し方だが、これは絶対値（ぜったいち）と偏角（へんかく）という概念からできているので、この二つと複素数の掛け算との関係を順に見ていこう。

複素数の絶対値

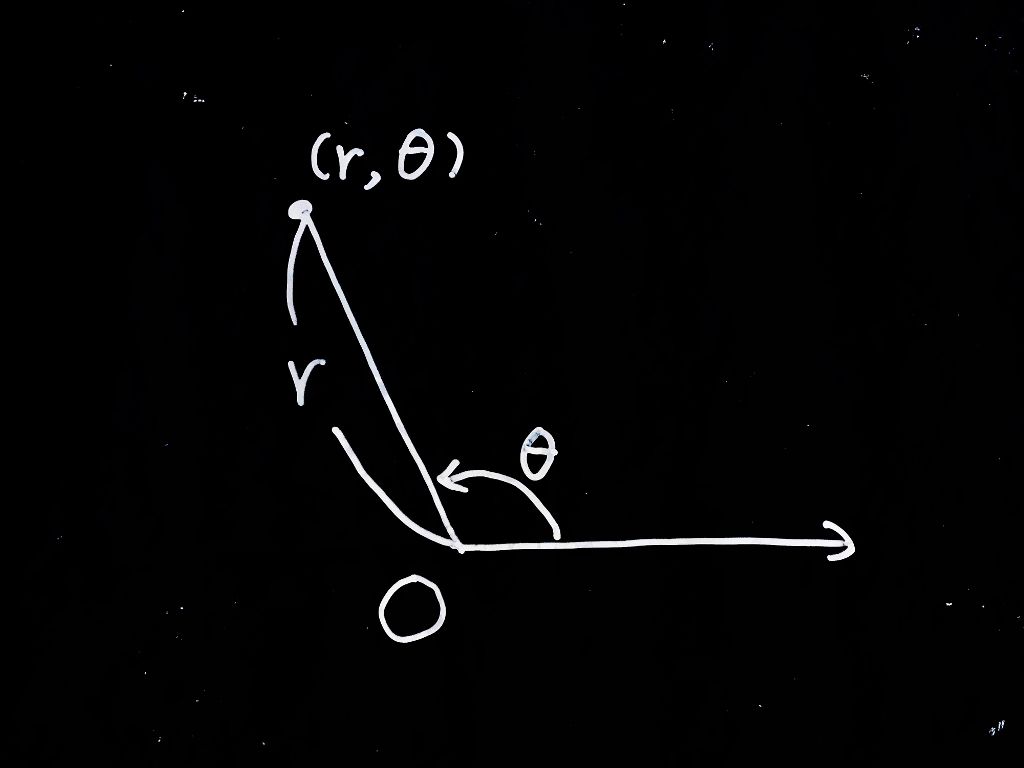
今、平面上に一つの複素数$z$があったとしよう。この$z$と原点$O$との距離のことを絶対値という。もし$z$が直交座標によって

$$z = x + yi$$

と表されていたなら、その絶対値（$|z|$と両側を縦線で挟んで表すことになっている）は

$$|z|=\sqrt{x^2+y^2}$$

となる。これは、三平方の定理から

$$|z|^2=x^2+y^2$$

となるからだ。（絶対値は、原点との距離だから正の数しか考えない。）

さて、複素数を二つ用意して、その掛け算の結果の絶対値を考えてみよう。すると、
\begin{align}
z = a + bi\\
w = c + di
\end{align}
としたとき、
\begin{align}
|zw|&=|(a + bi)(c + di)|\\
&= |(ac - bd) + (ad + bc)i|\\
&= \sqrt{(ac - bd)^2+ (ad + bc)^2}\\
&= \sqrt{a^2c^2 - 2abcd + b^2d^2 + a^2d^2+ 2abcd + b^2c^2}\\
&= \sqrt{a^2c^2+ b^2d^2 + a^2d^2+ b^2c^2}\\
&= \sqrt{(a^2+ b^2)c^2+ (a^2+ b^2)d^2}\\
&= \sqrt{(a^2+ b^2)(c^2 + d^2)}\\
&= |z||w|
\end{align}

このように絶対値同士は掛け算するとそのまま掛け算される！例えば絶対値が$\frac{1}{2}$と$2$の複素数があったら掛け算したら絶対値は$1$になるってことですよ。これすごくない？

これ、今$w$が逆数だったら割り算もできてるからね。

\begin{align}
1 &= |1| \\
&= \left|z\cdot\frac{1}{z}\right| \\
&= |z|\left|\frac{1}{z}\right|
\end{align}
よって
$$\left|\frac{1}{z}\right| = \frac{1}{|z|}$$
つまり
\begin{align}
\left|\frac{z}{w}\right| &= |z|\left|\frac{1}{w}\right| \\
&= \frac{|z|}{|w|}
\end{align}
おー、割り算もできたよー。例えば絶対値が$4$の複素数を絶対値が$3$の複素数で割ったら答えの絶対値は$\frac{4}{3}$になるってことですよ、先生。

掛け算には絶対値がすげー関わってるってことが想像できましたか？

複素数の偏角

平面上に複素数$z$があったとき、実軸の正の方向から測った原点を中心とする角度のことを偏角と言います。$\arg z$ と書きます。argumentの最初の三文字です。

どうしてここから角度を測るのかというのは、例えば
$$
\arg 1 = 0^\circ\\
\arg i = 90^\circ\\
\arg -1 = 180^\circ
$$

となることを考えると割と自然に感じてもらえるでしょうか。

それからこれは虚数の話(2)でやったことなんですが、例えば $2 + 4i$ という複素数があって、${\bf 2}$とか${\bf 4i}$とかぞれぞれの部分が回転すれば全体の ${\bf 2 + 4i}$ も同じだけ回転します。

今、$z$という複素数があり、絶対値が$1$、偏角が$\theta$（シータ）だとしましょう。こいつは$2$と$4i$を$\theta$だけ回転させる数だと分かります。なぜなら、

$$\arg z =\theta$$

$2$に$z$かけても偏角変わらないよね？

\begin{align}
\arg 2z &= \arg z \\
&= 0^\circ + \theta\\
|2z| &= |2||z| \\
&= |2|
\end{align}

絶対値が変わらずに角度が$\theta$だけ増えました。回転です。

じゃあ$4i$は？$4i$かけたら$90^\circ$回転するよ？

\begin{align}
\arg (z \cdot 4i) &= \theta +90^\circ\\
|4i \cdot z| &= |4i||z| \\
&= |4i|
\end{align}

やはり絶対値は変わっていないので角度$\theta$で回転してます。

というわけで
$$\arg (2 + 4i)z =\arg(2 + 4i) + arg z$$
もっと一般に、複素数$z$と$w$があったときに
$$\arg zw = \arg z + \arg w$$
です。

掛け算が足し算になっとるやないかい！そう、角度は足し算になるんです。それが複素数の掛け算の性質なのです。

逆数もやっておきましょう。
\begin{align}
0^\circ &= \arg 1 \\
&= \arg z \cdot \frac{1}{z} \\
&= \arg z + \arg \frac{1}{z}
\end{align}
「度」が気になりますが、思い切って次のように書いておきます。
$$\arg \frac{1}{z} = - \arg z$$
割り算は
$$\arg \frac{z}{w} = \arg z - \arg w$$
引き算になります。

複素数の極座標表示

平面上の複素数は絶対値と偏角が決まったら一つに決まります。絶対値を$r$、偏角を$\theta$として$(r, \theta)$のように書くとき、これを極座標表示と言います。

たださあ、これいわゆる式になってないんだよね。足し算とか掛け算とかでかけないからさあ。どっかにうまい方法はないものか。あるんだな、これが。

複素指数関数

$e$って知ってる？ネイピア数っていうんだけど...知らないかな？とりあえずこんな感じの式。
\begin{align}
e &= \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n\\
&= 2.7182818284...
\end{align}
ごめん、これ無理数だから割り切れないの。円周率とかと一緒で。だから式でしかかけないんだけど。うーん。どうしてこんなものが出てきたのか。まあ騙されたと思って。意味的には$n$が無限大に大きくなるときの右の式の値が$2.7$くらいってことです。

で、騙されたついでに全体を$i\theta$乗してみて欲しいんだよね。

\begin{align}
e^{i\theta} &= \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^{in\theta}\\
\end{align}
どうして虚数乗したの？バカなの？まあ落ち着けって。それで、
$$m = in\theta$$
とおくと$n \to \infty$の時$m$も無限大に向かうので、

\begin{align}
e^{i\theta} &= \lim_{m \to \infty} \left(1 + \frac{i\theta}{m}\right)^{m}\\
\end{align}
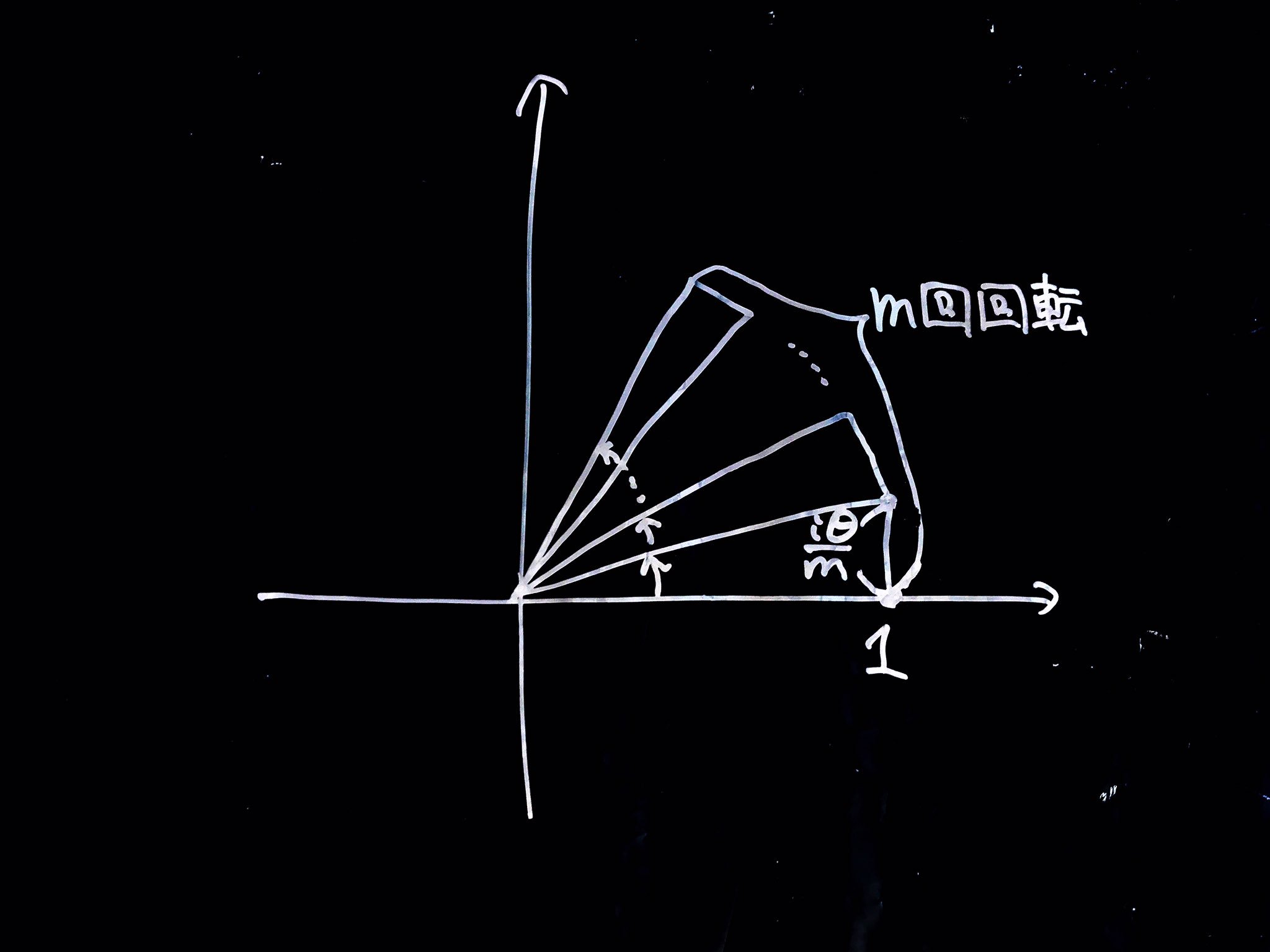
はい、こうなりました。かっこの中に注目してください。$1$はいいよね。$m$はとりあえずなんか整数だと思っておいて。で、$\frac{i\theta}{m}$だけ$1$から上に行くんだけど、そのあとそれを$m$乗するんだよ。偏角の話でいえば、$m$回回転するわけだ。

なんだかイビツなおうぎ形みたいになったけど、これさあ、弧の長さと中心角の大きさを同一視すれば（それはラジアンというやつだ。）、中心角${\bf \frac{\theta}{m}}$の扇型作って${\bf m}$個並べてるのと一緒じゃね？そして$m$が大きくなればイビツさは無くなり、

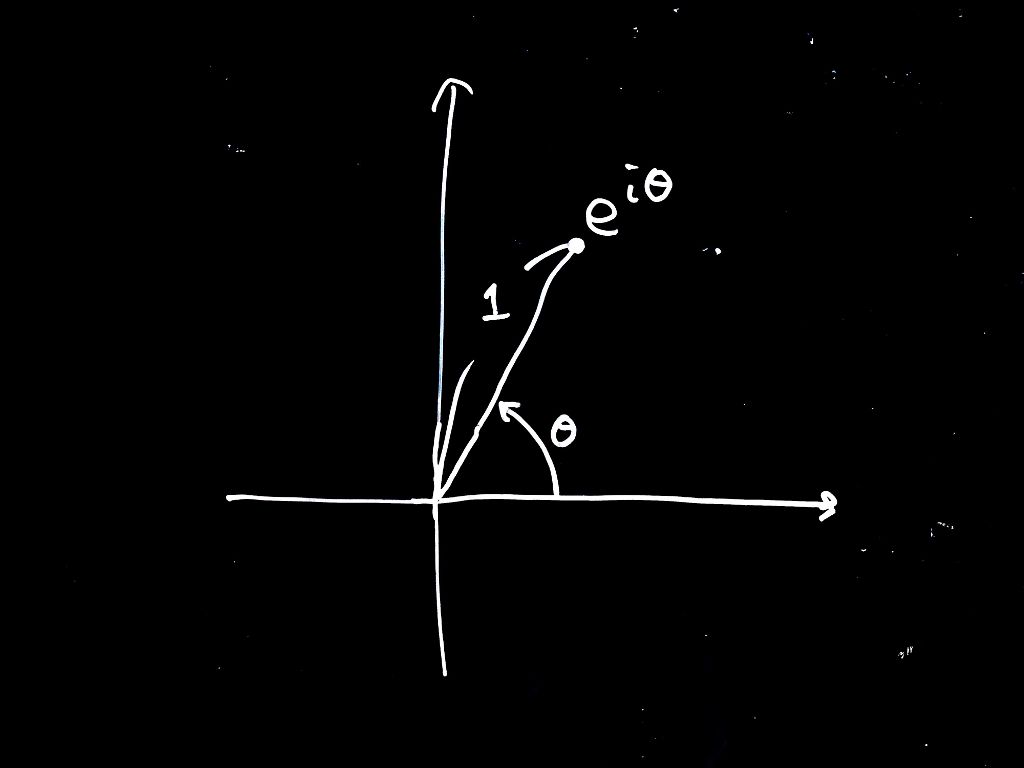
こうなる。（今後は全部角度はラジアンで考えます。というかまさにこのためにラジアンが存在するのだよ。）あとは、絶対値が$r$のときは$r$倍すればいいから、極座標で$(r, \theta)$と表された複素数の式は

$$re^{i\theta}$$

となるわけです。まとめると、複素数zがあったとき

$$z = |z|e^{i \cdot \arg z}$$

となりました。さあ掛け算してみよう。
$$
z_1 = r_1e^{i\theta_1}\\
z_2 = r_2e^{i\theta_2}\\
$$
のとき

$$z_1z_2 = r_1r_2e^{i(\theta_1+\theta_2)}$$

このように、複素数の掛け算では、絶対値は掛け算、偏角は足し算となりました。

複素解析という世界

今回、指数の部分に虚数を乗っけるとかいう暴挙をなんの前提もなく使いましたが、このように、本来すごく素朴なアイディアから発生したものです。数学的に厳密な部分は複素解析という分野できちんと議論することができます。複素解析では指数だろうが三角関数だろうが微分だろうが積分だろうが複素数をぶち込みます。そんなことしても崩れないでちゃんと綺麗な理論になってくれるところが数学の懐の広さ、面白さだと思っています。

練習問題

1. 複素数 $z = a + bi$ の共役複素数を $\overline{z} = a - bi$ と書くことにします。$|z|^2 = z\overline{z}$ を証明してください。

2. $e^{i\pi} + 1 = 0 $を証明してください。

3. 複素数 $z = a + bi $ に対し、

$$
\mathrm{Re}(z) = a\\
\mathrm{Im}(z) = b
$$
です。いま、
$$
\cos\theta = \mathrm{Re}(e^{i\theta})\\
\sin\theta = \mathrm{Im}(e^{i\theta})
$$
と定義します。加法定理
$$
\cos(\theta_1 \pm \theta_2) = \cos\theta_1\cos\theta_2 \mp \sin\theta_1\sin\theta_2\\
\sin(\theta_1 \pm \theta_2) = \sin\theta_1\cos\theta_2 \pm \cos\theta_1\sin\theta_2
$$
を証明してください。