虚数の話(2) 練習問題解答
虚数の話(2) 練習問題解答
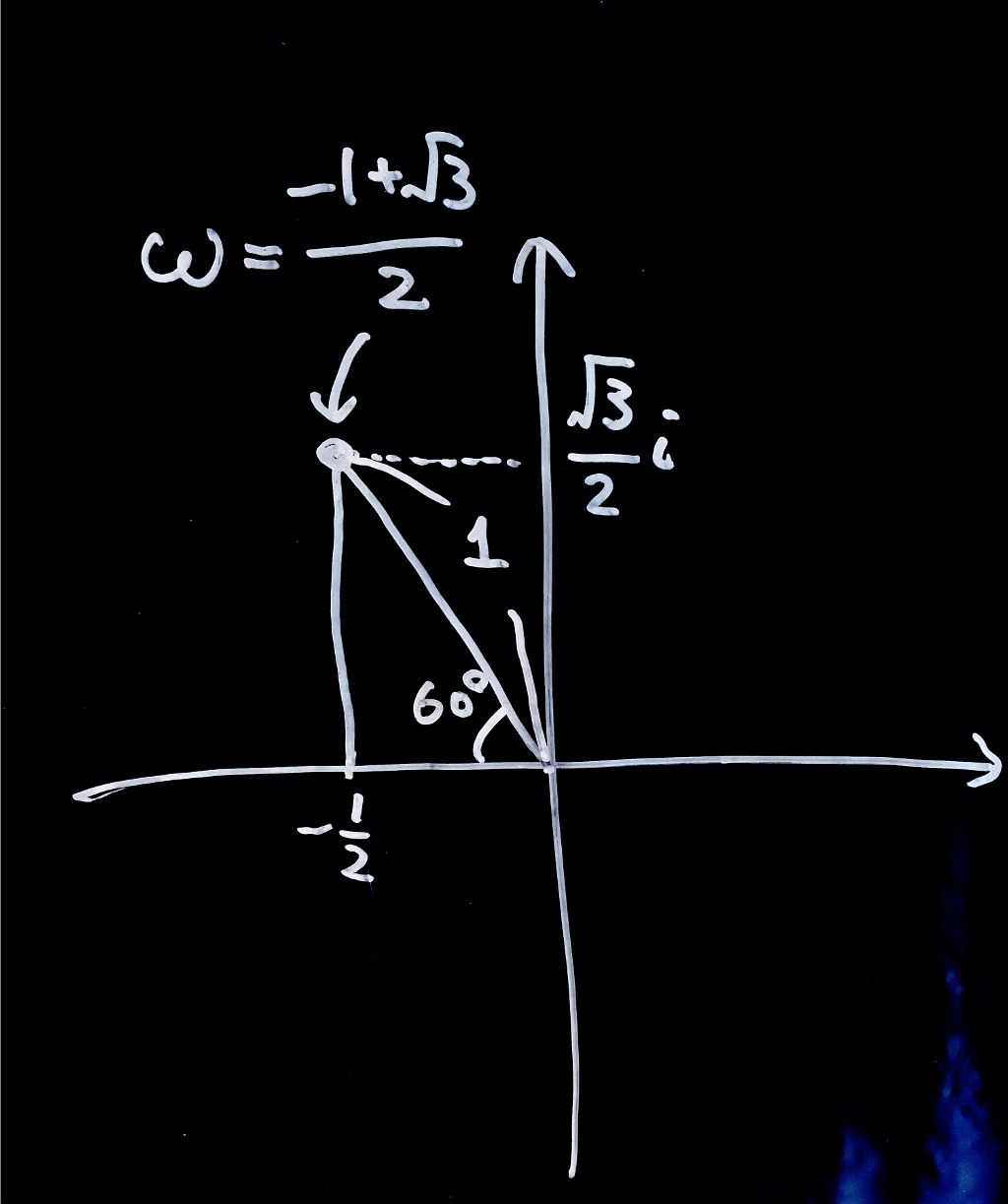
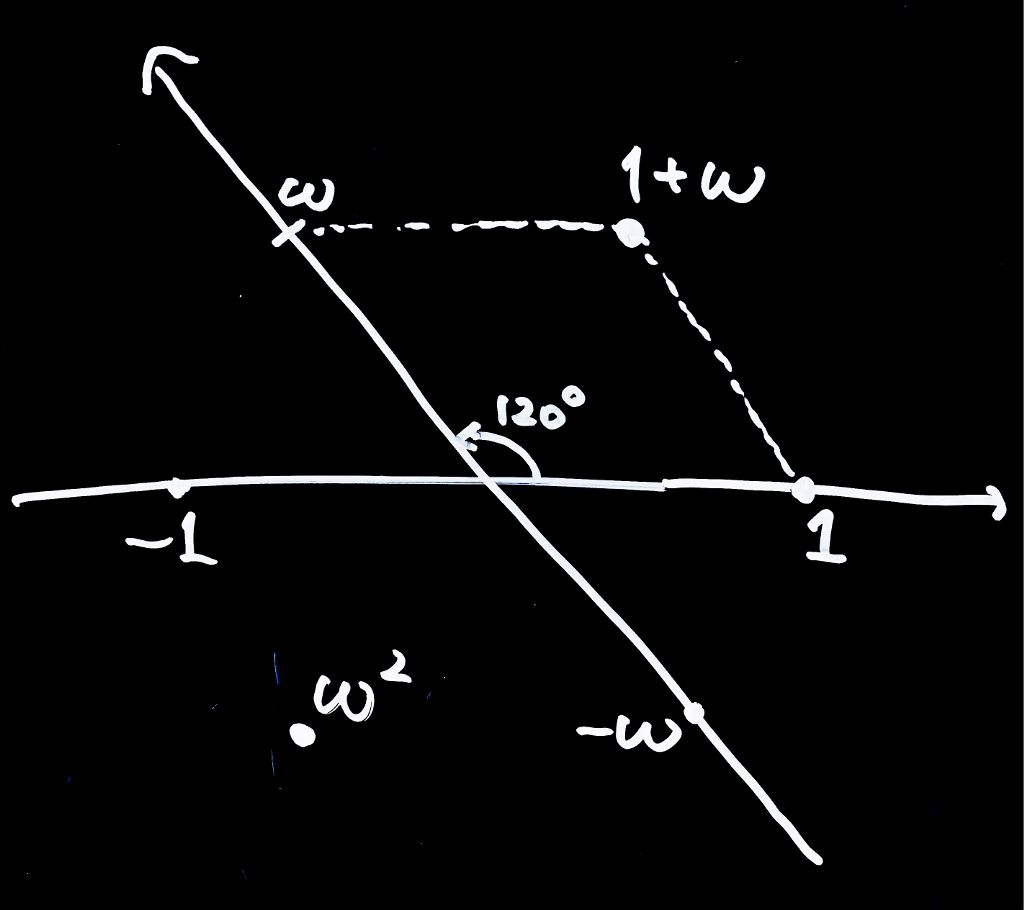
1. \(\omega = \frac{-1 + \sqrt{3}i}{2}\)とします。\(\omega\)を複素平面の上に書いてください。
念の為書いておきますが
\begin{align}
\omega &= \frac{-1 + \sqrt{3}i}{2} \\
&= -\frac{1}{2} + \frac{\sqrt{3}}{2}i
\end{align}
です。よって、
となります。
辺の比率が\(1:2:\sqrt{3}\)の三角形です、はい。
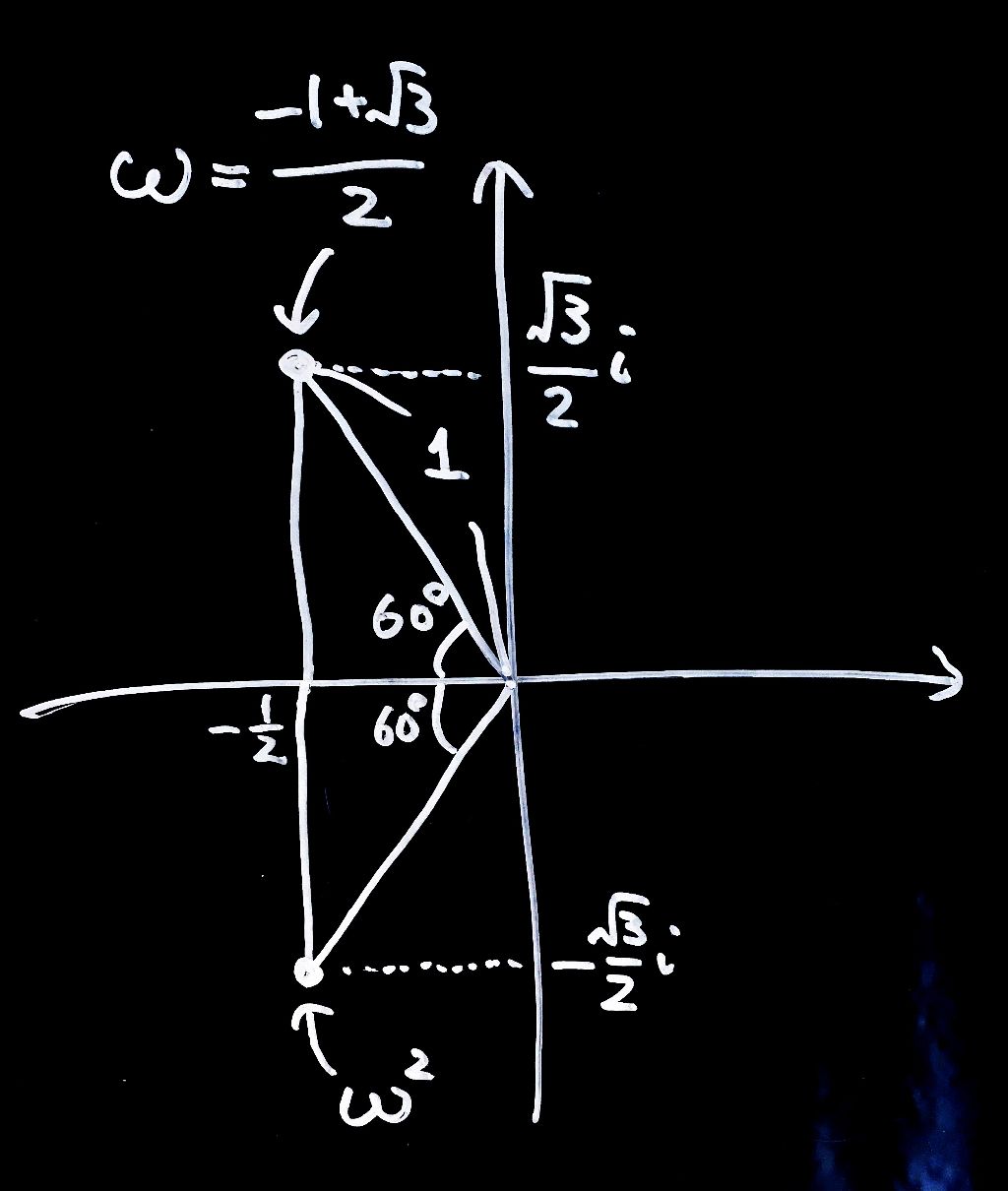
2. \(\omega\)の二乗を計算して、複素平面の上に書いてください。
\begin{align}
\omega^2 &= \left(\frac{-1 + \sqrt{3}i}{2}\right)^2\\
&= \frac{(-1 + \sqrt{3})i)^2}{4}\\
&= \frac{(-1)^2 + 2(-1)(\sqrt{3}i) + (\sqrt{3}i)^2}{4}\\
&= \frac{1 - 2\sqrt{3}i - 3}{4}\\
&= \frac{-2 - 2\sqrt{3}i}{4}\\
&= \frac{-1 - \sqrt{3}i)}{2}
\end{align}
ということで、
さっきの\(\omega\)を真下に反転させた形になりました。ちなみにこうやってある複素数を上下反転させることを複素共役(ふくそきょうやく)をとるといいます。今回たまたま\(\omega\)を二乗すると複素共役になった、ということです。角度が反転していることに注意してください。
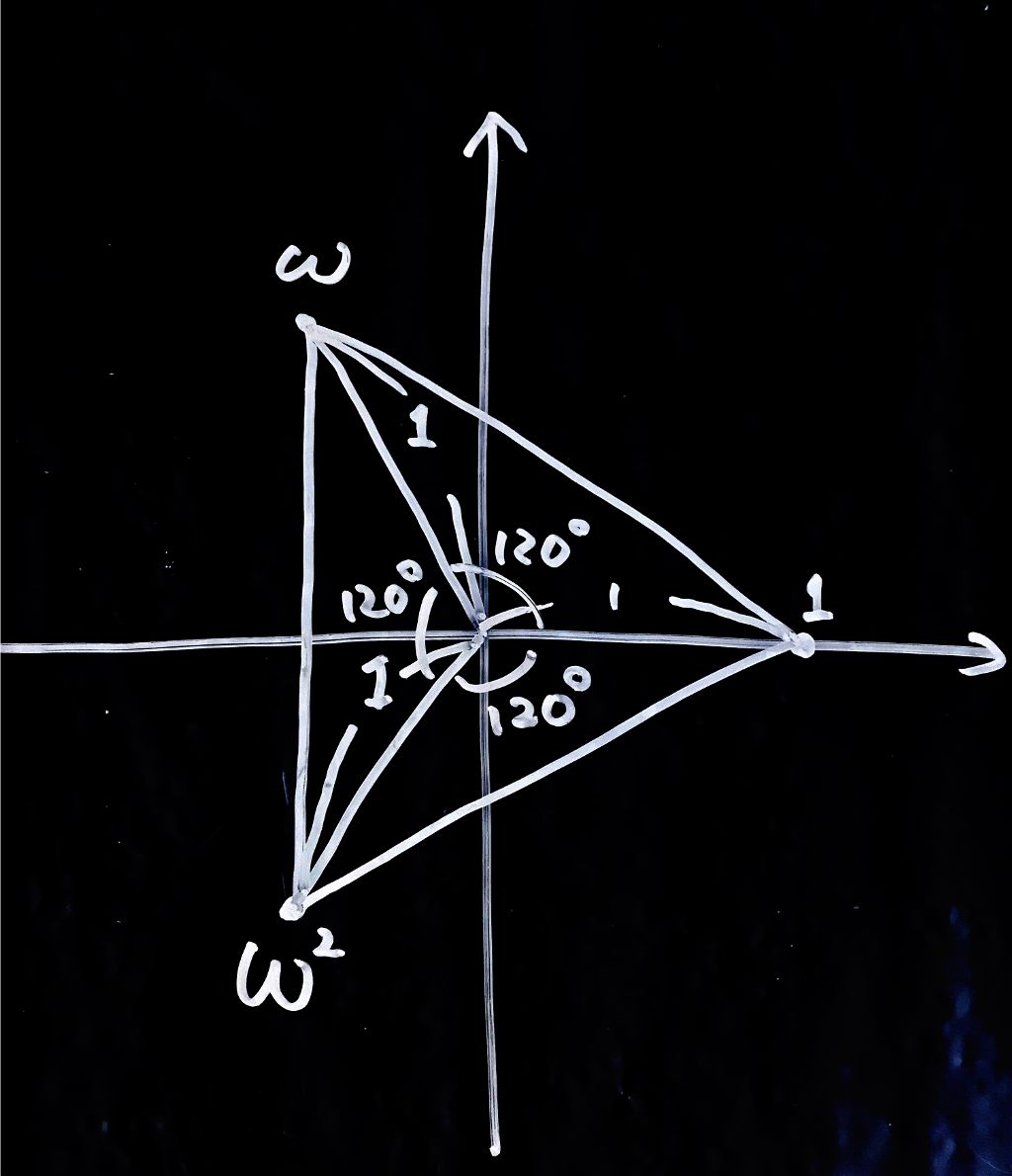
3.\(\omega\)の三乗を計算して、複素平面の上に書いてください。正三角形ができましたか?
さっきの結果にさらに\(\omega\)をかけましょう。
\begin{align}
\omega^3 &= \omega^2 \cdot \omega\\
&= \frac{-1 - \sqrt{3}i}{2} \cdot \frac{-1 + \sqrt{3}i}{2}\\
&= \frac{(-1 - \sqrt{3}i)(-1 + \sqrt{3}i)}{4}\\
&= \frac{(-1)^2 + (-1)\sqrt{3}i + (-\sqrt{3}i)(-1) + (-\sqrt{3}i)(\sqrt{3}i)}{4}\\
&= \frac{1 + 3}{4}\\
&= \frac{4}{4}\\
&= 1
\end{align}
綺麗に\(1\)になりました。図にしてみると\(\omega, \omega^2, \omega^3(=1)\) の三点で正三角形になっています。
結果としては\(\omega\)は三乗すると\({\bf 1}\)になる数、言い方を変えると\({\bf 120^\circ}\)回転する数、ということが分かります。
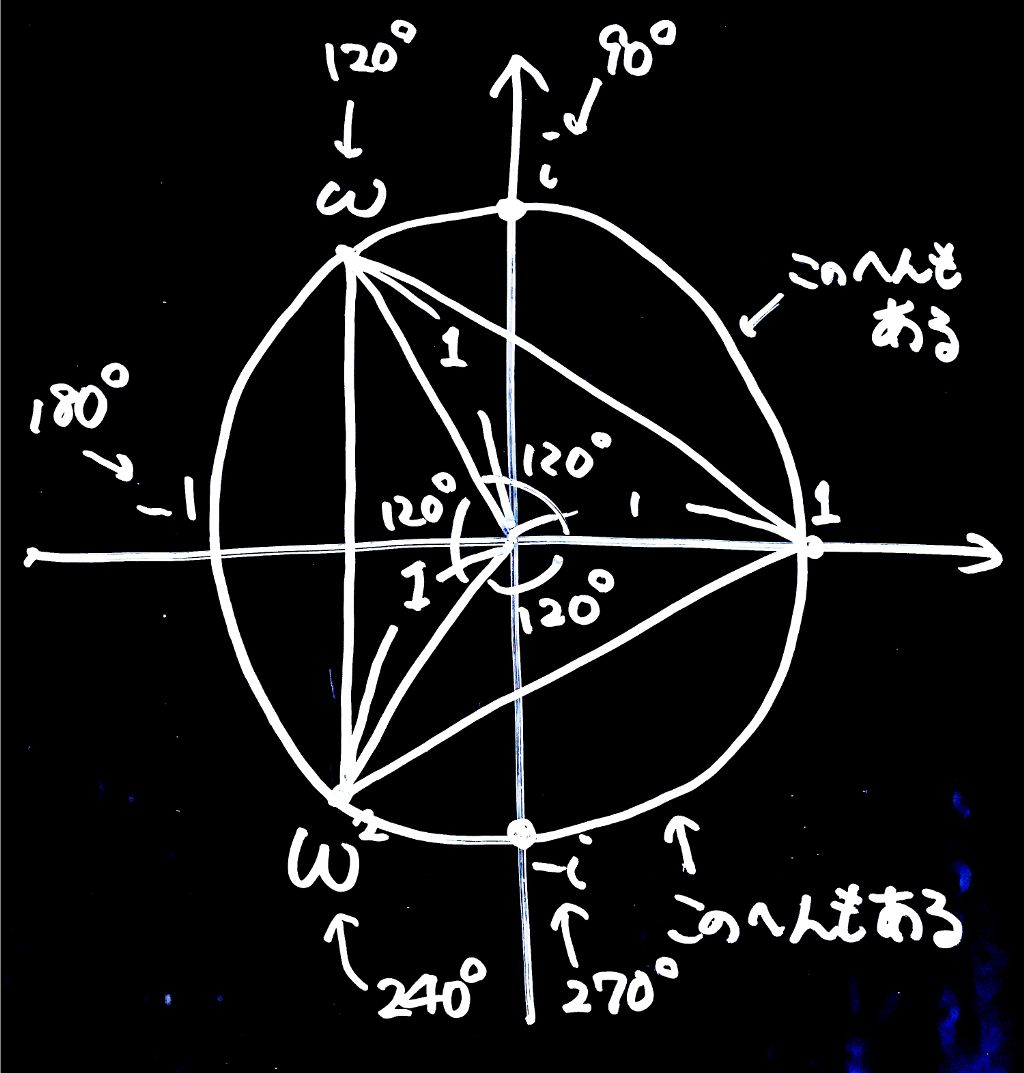
極端な話、単位円(半径1で中心が原点の円)上に点をとれば何度回転する数でも作れます。ていうかもう既に色々作りました。例えばωの二乗は\(240^\circ\)回転です。\(-i(=i^3)\)は\(270^\circ\)回転です。全部単位円上に乗っています。なんでもどんとこい。
4. \(a + bi\)の逆元は何ですか。\(c + di\)の形で答えてください。ただし、\(a, b, c, d\)はそれぞれ実数、\(a + bi \neq 0\)です。
複素数\(z\)を使って\( (a + bi)z= 1\)とします。すると、
\begin{align}
(a+bi)(a-bi)z&=a-bi\\
(a^2+b^2)z&=a-bi
\end{align}
ところで、\(a + bi \neq 0\)なので、\(a\)と\(b\)は同時に\(0\)になることがありません。よって\(a^2 + b^2 \neq 0\)です。これで割り算ができて、
$$
z=\frac{a}{a^2+b^2}-\frac{b}{a^2+b^2}i
$$
となります。求める\(c+di\)の形になりました。ちょっと書き換えると
$$\frac{a - bi}{a^2 + b^2}$$
です。少しここで考えてみてほしいことがあります。
分母は実数になっています。本体は分子です。これは\(a + bi\)に対して\(a - bi\)ですから複素共役です。回転角度が逆向きになっています。逆元、と言うくらいですからね、これが
いいところですね。
5. 三次方程式 \(x^3 = 1\) を解いてください。解は三つあります。
「三次方程式なんだから三つ解があるのは当たり前だろう」とか言わないでください。そりゃ5つも6つも出てきたら困りますが、例えば、\(x^3 = 0\) の解は \(x = 0\) だけです。三重解というやつです。今回はそういうのじゃないので \(x = 1\) だけ見つけて満足しないでねってことです。
頑張って因数分解しましょう。
\begin{align}
x^3 = 1\\
x^3 - 1 = 0\\
(x - 1)(x^2 + x + 1) = 0\\
(x - 1)(x - \frac{-1 + \sqrt{3}i}{2})(x - \frac{-1 - \sqrt{3}i}{2}) = 0\\
x = 1, \frac{-1 + \sqrt{3}i}{2}, \frac{-1 - \sqrt{3}i}{2}\\
\end{align}
これで答えは終わりですが、要するにこれ\(\omega\)ですね。
$$x = 1, \omega, \omega^2$$
三乗したら1になる数はこの三つです。「1とωは三乗したら1になるけど最後のは?」と思ったら計算してみましょう。はい。
\begin{align}
(\omega^2)^3 &= \omega^{2\times3}\\
&= (\omega^3)^2 \\
&= 1^2\\
&= 1\\
\end{align}
なりました!
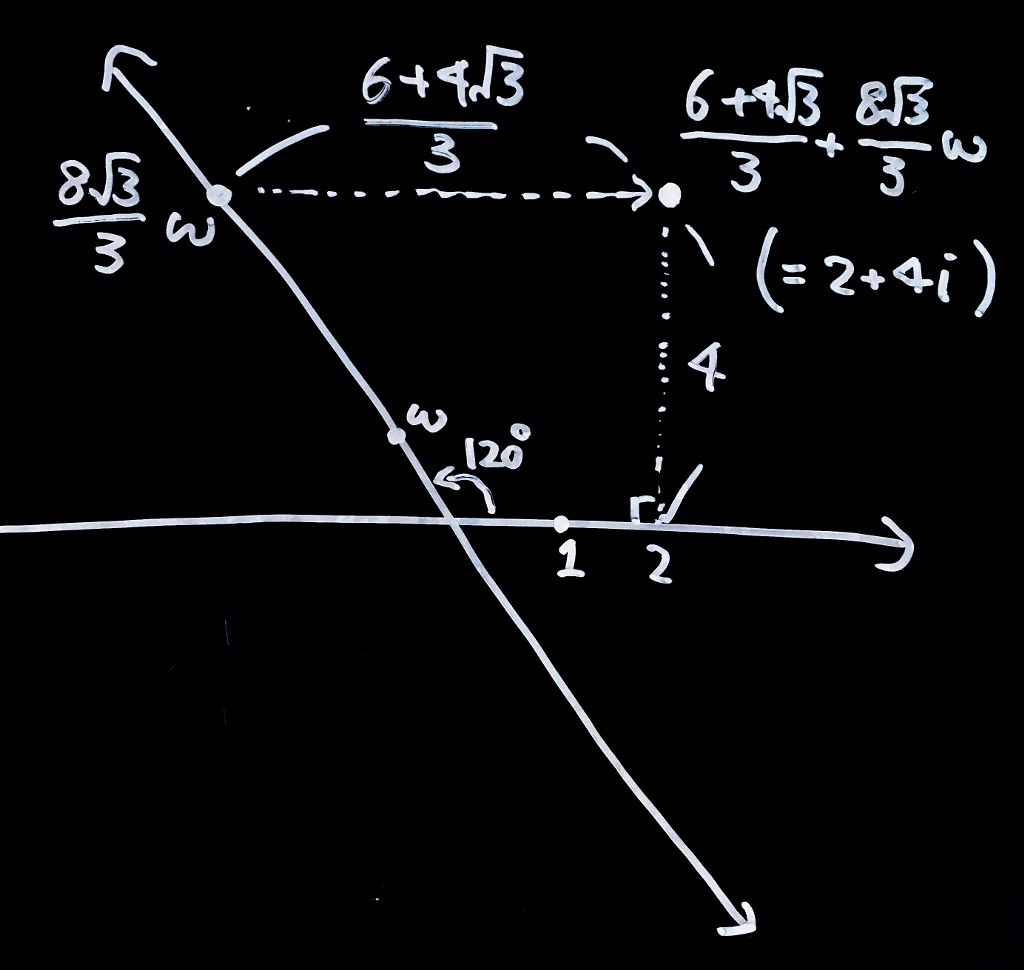
6. 掛けると\(120^\circ\)回転する数\(\omega\)を実数に付け加えて\( (1, \omega)\)平面を作ってください。そこに、\(2+4i\)を\(\omega\)で表して書き込んでください。
まず、\( (1, \omega)\)平面なんて言い方は公式には存在しないからすいません。
でも、\(1\), \(i\)の二つの要素で平面を作った時の要領で、\(1\)と\(\omega\)でもやったらいいんです。
こう。
ね、意外と可愛いでしょ?(爆)
さて、\(2 + 4i\) を\(\omega\)で表したいんですが、まずは\(i\)を\(\omega\)で表しましょう。
\begin{align}
\omega &= \frac{-1 + \sqrt{3}i}{2}\\
2\omega &= -1 + \sqrt{3}i\\
i &= \frac{2\omega + 1}{\sqrt{3}}\\
\end{align}
できました。
では、
\begin{align}
2 + 4i &= 2 + 4 \cdot \frac{2\omega + 1}{\sqrt{3}}\\
&= \frac{2\sqrt{3} + 4 + 8\omega}{\sqrt{3}}\\
\end{align}
これでもいいんですが、図に書けないので(死)、分子を\(\omega\)とそれ以外に分けてから分母を有理化しましょう。
\begin{align}
2 + 4i &= \frac{2\sqrt{3} + 4}{\sqrt{3}} + \frac{8}{\sqrt{3}}\omega\\
&= \frac{6 + 4\sqrt{3}}{3} + \frac{8\sqrt{3}}{3}\omega\\
&= 4.3... + 4.6...\times\omega\\
\end{align}
だいたいこんな感じになりました。
言いたかったのは別に\({\bf i}\)じゃなくて\({\bf \omega}\)でも複素平面は作れるよってことです。とはいえ私たちは直角に支えられて生きています。明日から\(120^\circ\)でモノ考える世界ってのは、ちょっと勘弁願いたいですね。
7. 次の三項間漸化式を解いてください。
\(a_0 = 1, a_1 = 1, a_{n+2}= - a_{n+1} - a_n (n \geq 0)\)
$$a_{n+2}= - a_{n+1} - a_n$$
より、
$$a_{n+2}+ a_{n+1} + a_n = 0$$
\(\omega = \frac{-1 + \sqrt{3}i}{2}\) と置と、\(\omega, \omega^2\) は\(x^2 + x + 1 = 0\) の解なので、
$$
-(\omega + \omega^2) = 1\\
\omega \cdot \omega^2 = 1
$$
よって、
$$a_{n+2} - (\omega + \omega^2)a_{n+1} + (\omega \cdot \omega^2)a_n = 0$$
ここから二通りの式が作れて、まず
$$a_{n+2} - \omega a_{n+1} = \omega^2(a_{n+1} - \omega a_n)$$
だから
\begin{eqnarray}
a_{n+2} - \omega a_{n+1} &=& (\omega^2)^{n+1}(a_1 - \omega a_0) \nonumber \\
&=& (\omega^2)^{n+1}(1 - \omega) \tag{1}
\end{eqnarray}
同様に、
$$a_{n+2} - \omega^2 a_{n+1} = \omega(a_{n+1} - \omega^2 a_n)$$
だから
\begin{eqnarray}
a_{n+2} - \omega^2 a_{n+1} &= &\omega^{n+1}(a_1 - \omega^2 a_0) \nonumber \\
&=& \omega^{n+1}(1 - \omega^2) \tag{2}
\end{eqnarray}
\( (1)\times \omega - (2)\)より
\begin{align}
(\omega - 1)a_{n+2} &= (\omega^2)^{n+1}(1 -\omega)\omega -\omega^{n+1}(1 -\omega^2)\\
&= (\omega^2)^{n+1}(1 -\omega)\omega -\omega^{n+1}(\omega - 1)\omega^2
\end{align}
よって
\begin{align}
a_{n+2} &= - (\omega^2)^{n+1}\omega -\omega^{n+1}\omega^2\\
&= - ω^{2n} - ω^n
\end{align}
数字を付け替えて、\(n\geq 2\)のとき、
\begin{align}
a_{n} &=- ω^{2(n-2)} - ω^{n-2}\\
&= - ω^{2n+2} - ω^{n+1}
\end{align}
これは、\(n = 0, 1\)のときも成り立つ。
したがって、\(n\geq 0\)のとき
\begin{align}
a_{n} &= - ω^{2n+2} - ω^{n+1}
\end{align}
解説
三項間漸化式は特性方程式が二次方程式なので、虚数解になることがある。そのため一般項の計算式には虚数が入り込むが、初期条件と漸化式から考えて、計算結果は実数だ。しかも整数。お時間があったらこの数列がどんな風になるか実際に計算してみてください。
8. \(x = a + b\omega (a, bは実数)\)に対して\(f(x)\)を \(f(x) = a + b\omega^2\)で定義します。複素数\(z\)が\(n\)次方程式 \(a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 = 0 (a_iは実数)\)の解である時、\(f(z)\)も解であることを示してください。
いま、任意の複素数を\(x + yi(x, yは実数)\)で表すと、
\begin{align}
x + yi &= x + y \cdot \frac{2\omega + 1}{\sqrt{3}}\\
&= x + \frac{1}{\sqrt{3}} + \frac{2y}{\sqrt{3}}\omega
\end{align}
よって任意の複素数は \(a + bω (a, bは実数)\)の形で表せる。
次に、
$$f(\omega^2) = f(-1-\omega) = -1-\omega^2 =\omega$$
また、\(z = a + bω, w = c + dω\) を任意の複素数、\(k, l\)を任意の実数とするとき、
\begin{align}
f(kz + lw) &= f(k(a + b\omega) + l(c + d\omega))\\
&= f(ak + cl + (bk + dl)\omega)\\
&= ak + cl + (bk + dl)\omega^2\\
&= k(a + b\omega^2) + l(c + d\omega^2)\\
&= kf(z) + lf(w)\\
f(z \cdot w) &= f{(a + b\omega)(c + d\omega)}\\
&= f(ac + bd\omega^2 + (bc + ad)\omega)\\
&= ac + bd\omega + (bc + ad)\omega^2\\
&= ac + bd\omega^4+ (bc + ad)\omega^2\\
&= (a + b\omega^2)(c + d\omega^2)\\
&= f(z)f(w)
\end{align}
さて、複素数\(z\)が\(n\)次方程式 \(a_nx^n + a_{n-1}x^{n-1} + ... + a_1x + a_0 = 0 (a_iは実数)\)の解であるとき、
\begin{align}
0 &= f(0) \\
&= f(a_nz^n + a_{n-1}z^{n-1} + ... + a_1z + a_0)\\
&= a_nf(z)^n + a_{n-1}f(z)^{n-1}+ ... + a_1f(z) + a_0
\end{align}
よって\(f(z)\)もこの方程式の解である。
解説
よく、このような問題が複素共役についてなされますが、今回は\(\omega\)でそれを説明してみました。単に複素共役だからってやるともっとすんなり答えになっちゃうんだけどそれは許してください。