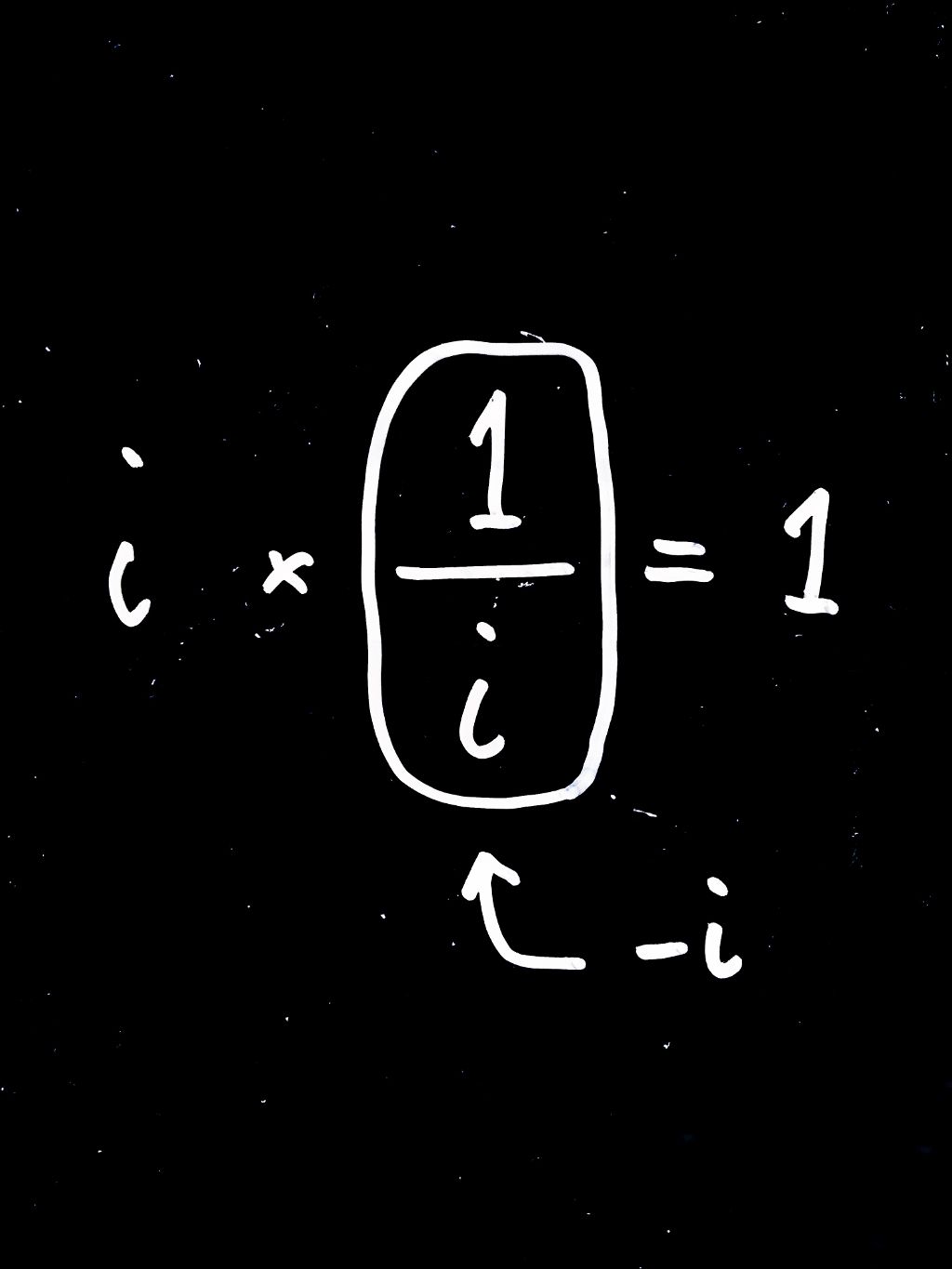虚数の話(1) 練習問題解答
前置き
数学の話をするときに、避けては通れないのが、いわゆる筆記というか、ノートというか、とにかく自分の頭の中を文章としてアウトプットする作業である。レポートといってもいい。これが大事だ。当たり前だが、数学は学問なので、それなりの客観性を担保する必要がある。そのためには何語でもいいから文章に書き起こす必要がある。
たまに、ノートを取りたくない、という人がいる。私も塾で教えていた時に一人そういう生徒に出会った。そこまで行かなくても、誰かから数学の話を聞くだけなら自分はノートなんて書かなくてもいいじゃないかと思うひとは多いだろう。(会社なんていったら、自分がどんなに頑張って資料を用意したところで偉い人はメモ一つ取ってくれない。そういう人に限って前と違うことを平気で言う。失礼、これは違う話だった。)
話を戻そう。
思うのだが、自分の考えをアウトプットしたり整理したりするには書くのが一番だ。紙でもパソコンでも構わない。絵でも図でもいい。とにかく記録媒体に残っていて、別の人間が「合ってる」とか「間違ってる」とか指摘できる形がいい。そうしないと自分でもほとんど批判できない。
高名な数学者でさえ、「それなら多分証明できますよ。」と言っていて、実際に証明にまとめてみたら証明になっていなかった、ということはある(もっとも、本当に優秀な人なら、最初に考えたアイディアがまずかっただけで、どうせ証明はそのうち完成する)。そのくらい頭の中の考えはふわふわしていて、不確かなものだ。自分に数学のような確かなものが根付いたかどうかは、数学の証明がどれだけ書けるようになったかで大体測れるのではないだろうか。
もう一つ指摘しておくことがある。人間はインプットとアウトプットのバランスを保った方がいい。私がある量の数学を提供したら、自分でほんの簡単な内容でも構わないから、同じ量の数学を書き出した方がいい。インプットだけでも、アウトプットだけでも行き詰まってしまう。詰まる所、『学びて思わざれば則ち罔し、思いて学ばざれば則ち殆うし』という言葉に尽きる。仲の良かった数学科の友人が大切にしていた言葉だが(彼は特別優秀だった)、僕も大事にしたいと思う言葉だ。
ところで、証明問題でない数学の問題は存在しない。計算だけの問題だって厳密には証明のテクニックを至る所で使っている。
では問題の解説をしよう。
虚数の話(1) 練習問題解答
1. \({\bf i}\)の\({\bf100}\)乗を計算してください。
\begin{align}
i^{100} &= i^{4\times25} \\
&= (i^4)^{25} \\
&= 1^{25} \\
&= 1
\end{align}
解説
こういうの(やけにでかい数の計算)が思いつかないときは、とにかく計算が可能なあたりの数字を当てはめて試しに計算してみるのがいい。
\begin{align}
i^1 &= i\\
i^2 &= -1\\
i^3 &= -i\\
i^4 &= 1\\
i^5 &= i\\
i^6 &= -1\\
i^7 &= -i\\
i^8 &= 1\\
...
\end{align}
四回周期で\(4\)の倍数の時はいつも\(1\)だということに気づいただろうか?
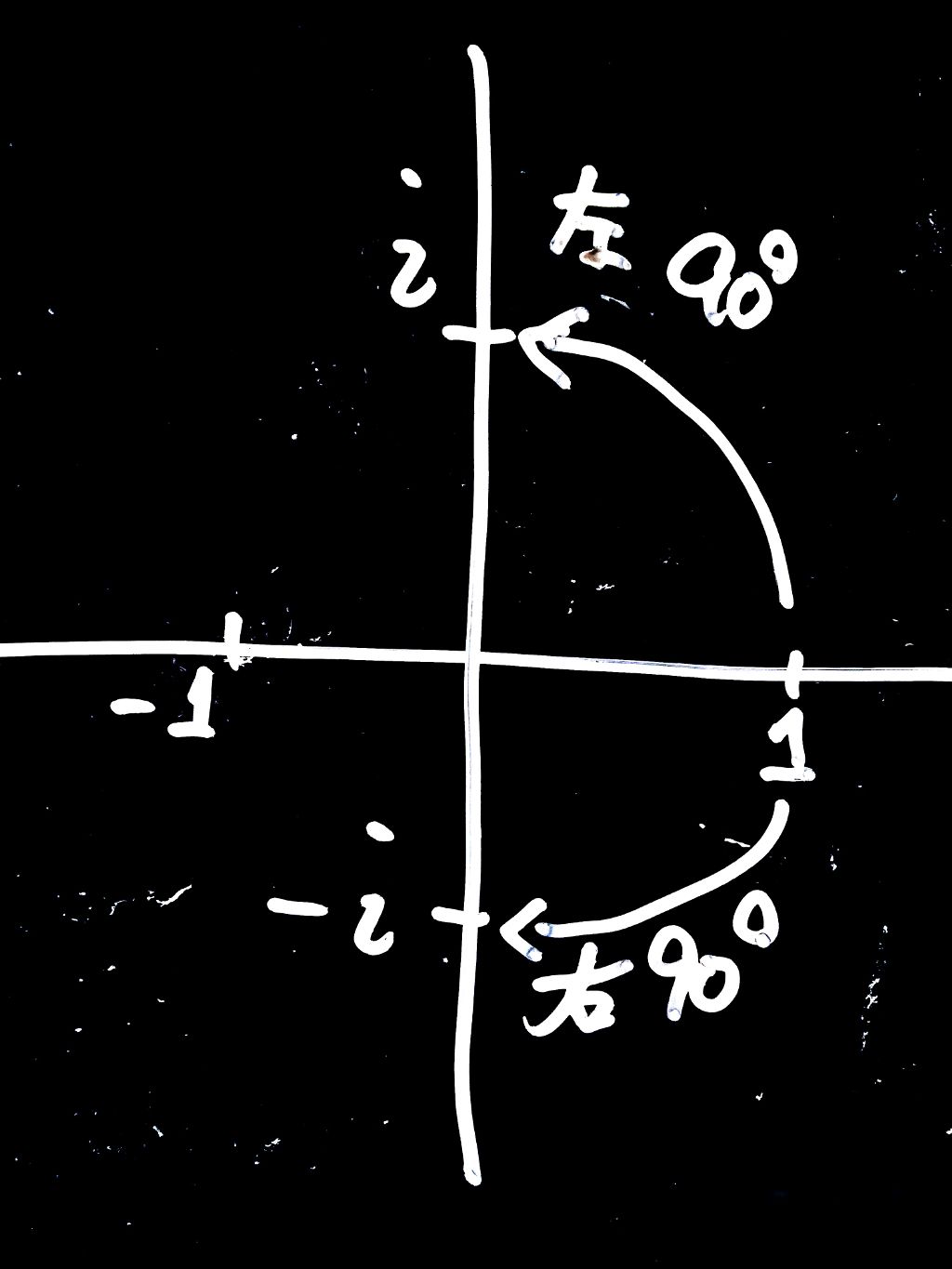
この計算は意味的には\(90\)度回転を\(4\)回繰り返したら\(360\)度回転して、何もしないこと(\(1\)倍は何もしないこと!)を示す、ということになる。あとは、\(i\)が\(100\)個並んでいるところを想像して、\(4\)個ずつグループにするところ、
\begin{align}
iiiiiiiiiiiiiiiiiiiiiiiiiii......iiiiiiiiiiiiiiiiiiiiiiiii &→ i^{100}\\
(iiii)(iiii)(iiii)......(iiii)(iiii)(iiii) &→ (i^4)^{25}\\
(1)(1)(1)...(1)(1)(1) &→ 1^{25}\\
1 &→ 1
\end{align}
が想像できればよろしい。
\(25\)が正直どうでもいいというのが伝わるだろうか。
2.「\({\bf2}\)乗したら\({\bf-1}\)になるけど\({\bf5}\)乗したら\({\bf1}\)になる数」なんてものが存在してはいけない理由として、もしそんな数(仮に\({\bf X}\)としましょう)が存在すると\({\bf1 = 0}\)が証明できます。やって見てください。
\begin{align}
X &= X\\
X^{10} &= X^{10}\\
(X^2)^5 &= (X^5)^2\\
(-1)^5 &= 1^2\\
-1 &= 1
\end{align}
両辺から\(1\)を引いて
$$-2 = 0$$
両辺を\(-2\)で割って
$$1 = 0$$
解説
だいたいいつも世界が崩壊すると\(1 = 0\)(全てゼロ)が証明できます。
3. \({\bf 1}\)を\({\bf i}\)で割った答えを考えてください。
\begin{align}
1 &= i^4 \\
&= i \times i^3 \\
&= i \times (-i)
\end{align}
よって
$$\frac{1}{i} = -i$$
解説
割り算、というと、「えっとお、\(1\)を\(i\)個に分けるってことはあ。。。」と考えた御仁もいらっしゃるかもしれないが、そういう考えは捨ててください。
割り算は掛け算とペアで出てくる存在だが、よくよく考えると、すでに\({\bf i}\)による掛け算がいくつかの同じものを用意するという概念から遠ざかっている。私たちは掛け算と言いながらよくわからない計算をしているのだ。
虚数の話を始めるより前からそういう場面には出会っているのではないだろうか?ベクトル同士を掛けるとか(内積というやつだ)。というか、分数の掛け算だって何個分みたいな話では説明がつかないはずだ。\({\bf -1}\)を掛けるってのは?どっこいしょ!これに「何個分」という意味はない!
実は掛け算、というより、この
$$\times$$
という記号が示しうる意味の幅はめっちゃ広い。だからそれに対応する割り算の定義も、同じ数だけ広い意味になると言って差し支えない。ただ、掛け算の意味が決まれば割り算の意味も基本的には決まる。それは、逆元、という考え方だ。いわゆる逆数という言葉と同じだと考えて当座は困らない。
例によってめっちゃ大雑把に言おう。
\(1\)割る\(3\)を考える代わりに三分の一っていう数を考えよう。それが\(3\)の逆数だよ!\(3\)と\(3\)の逆数を掛けると\(1\)になるよ!式で言うと、
$$1 = 3 \times \frac{1}{3}$$
と言うことだ。これで、\(3\)で割る代わりに\(\frac{1}{3}\)を掛ければいい。
だいぶ回り道をしたが、「\(1\)を\(i\)で割る」と言う代わりに「\(i\)の逆数(逆元)」を考えよう。かけ合わせると\(1\)になる、と言うのだから、さっきの\(i^4\)が役に立つ。
ところで、これも意味を考えてみると、\(i\)倍するのが(左向きの)\(90\)度回転だったが、\(-i\)倍は\(270\)度回転、つまり、右向きの\(90\)度回転だ。そう考えると確かに、逆、というイメージがぴったりくるのではないだろうか?
もちろん、左と右に\(90\)度回転をすれば、元に戻る。すなわち、\(i × (-i) = 1\) というわけだ。この式、当たり前に見える?